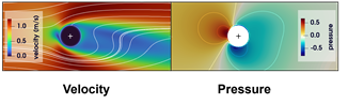
固体境界が埋め込まれた流れ場の基礎方程式として改良ナビエ・ストークス方程式を用いた数値解法をFortran90で実装したサンプルプログラム（R&B法 適用）
出典：
第38回数値流体力学シンポジウム（2024.12.11-13）
「マルチカラー法によるポアソン方程式SOR解法の加速化と境界埋め込みナビエ・ストークス方程式への適用」
大島 伸行、中道 信人（北海道大学）、白井 信裕（株式会社メトロ）
https://eprints.lib.hokudai.ac.jp/dspace/handle/2115/89344
995 !$acc kernels
996 !$acc loop independent
997 do i = 0, m+1
998 !$acc loop independent
999 do j = 0, n+1
1000 p_old(i, j) = p(i, j)
1001 end do
1002 end do
1003 !$acc end kernels
1006 !$acc kernels
1007 !$acc loop independent
1008 do k = 2, m*n, 2 ! even space
1009 j = (k - 1) / m + 1
1010 i = k - (j - 1) * m
1011
1012 !-- IF m is EVEN (Based on Column-Major Order; FORTRAN)
1013 if(mod(m,2)==0 .and. mod(j,2)==0) i = i - 1
1014
1015 p(i, j) = ( bb(i, j) &
1016 - ae(i, j) * p_old(i+1, j) - aw(i, j) * p_old(i-1, j) &
1017 - an(i, j) * p_old(i, j+1) - as(i, j) * p_old(i, j-1) ) &
1018 / ap(i, j) * relux_factor &
1019 + p_old(i, j) * (1. - relux_factor)
1020 end do
1021 !$acc end kernels
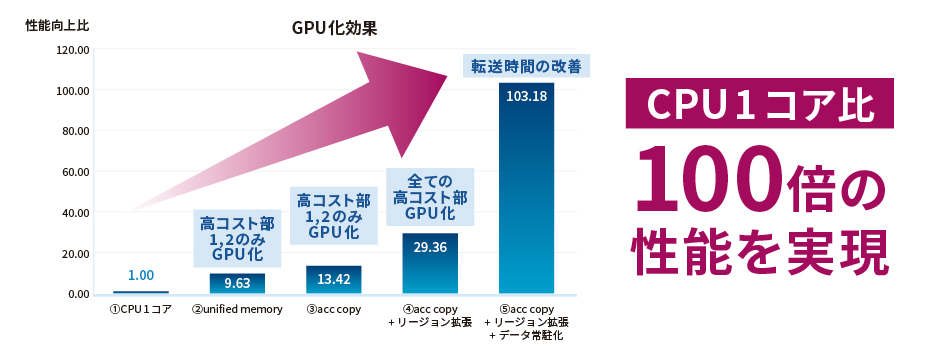
本資料では、 弊社技術の一端として「 GPU化による高速化事例」をご紹介します。
弊社は、ご記入いただく個人情報を、以下の目的に利用します。
弊社では、利用目的の達成に必要な範囲内において、他の事業者へ個人情報を委託することがございます。その場合は、個人情報保護体制が整備された委託先を選定するとともに、個人情報保護に関する契約の締結や適切な監督を行います。
弊社は、お客様の承諾を得た場合または法令により許された場合を除き、お客様の個人情報を第三者に提供いたしません。お客様の同意のもとまたは法令に基づき個人情報を第三者に提供する場合には、適切な管理を義務づけ、その第三者からの漏えい・再提供の防止などを図ります。
弊社に個人情報を提供することは任意です。ご提供いただけない場合は、弊社の業務に支障を来し、ご本人が弊社からの十分なサービスを受けられない可能性がございますのでご了承ください。
※開示、訂正、利用停止等のお申し出は、下記リンクに記載の受付窓口までご連絡ください。
https://www.metro.co.jp/privacypolicy-3.html◆「個人情報保護ポリシー」「プライバシーポリシー」をご覧になりたい方は下記リンクをご参照ください。
https://www.metro.co.jp/privacypolicy.htmlフォームが表示されない場合は、Q&Aをご覧ください。
GPUは非常に高いポテンシャルがある一方で、そのポテンシャルを持て余しているケースが数多くみられます。
メトロは30年以上に渡るコンパイラ開発やプログラム高速化の知見により、GPUを使ったアプリケーションの高速化を実現し、みなさまの研究・開発をスムーズに進める支援をします。
お客様の研究や開発における課題解決を支援します。一般的なアプリにはない機能の開発や、論文の計算手法の実装などを行います。
まずはお気軽にお電話またはフォームからお問合わせください